One of the most fundamental arithmetic skills to learn is how to calculate fractions. Know how to recognize components and kinds of fractions before you start working with them. After that, you can start subtracting and adding them. Understand how to divide and multiply for more complicated computations. Most of the time, you will need to simplify or lower the portion as well.
In this article, I will help you learn the ten simple ways to calculate fractions. An online fraction calculator is also recommended to help this process be more straightforward.
Fraction Calculator
Choose any mode you want to calculate. E.g Add Fraction of 1/2 + 3/4
Check and Uncheck the “Simplify” checkbox to simply numbers.
Display
Decimal
Add
Subtract
Multiply
Divide
Simplify
Looking for an easy way to calculate fractions? Check out the percentage calculator on Hood MWR. This calculator not only allows you to convert fractions to percentages, but it also helps you determine ratios and calculate percentage change. It’s a must-have tool for anyone who needs to work with percentages frequently, such as students, teachers, and business professionals.
So, What Are Fractions?
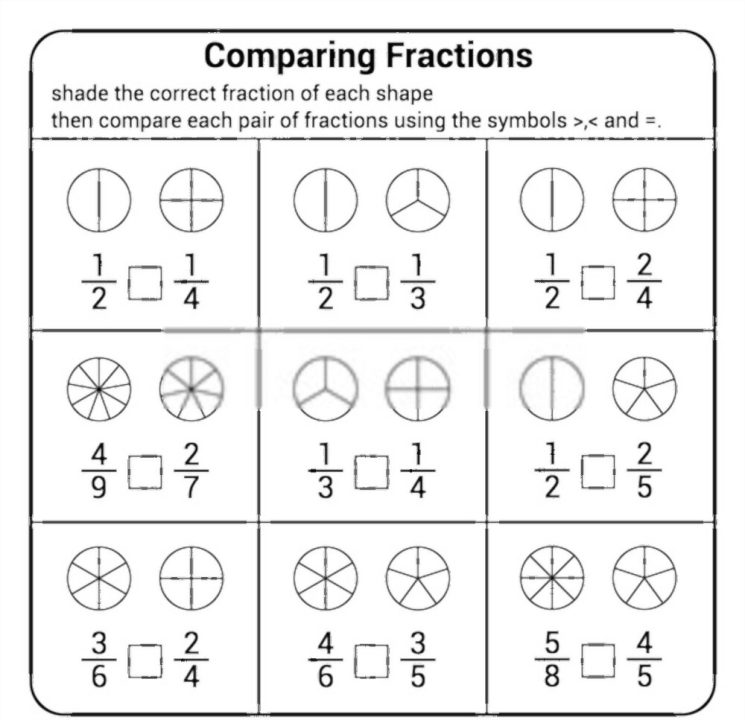
Fractions are numbers that indicate values that are less than one. Fractional numbers, sometimes referred to as whole numbers, are widely used to measure portions of a whole, for instance:
- 1/2: one half
- 1/5: one fifth
- 2/3: two thirds
Two numbers, one number is above, and the other is below with a dividing line, making up a fraction.
The denominator is considered under number, and it refers to the individual elements of the whole.
We usually utilize ordinal numbers to refer to the denominator, which are numbers that indicate a position, such as ”fourth” or ”fifth.”
The numerator, on the other hand, is considered the top number in a fraction, and it indicates how many pieces of the total we are working with.
Imagine a cake that is evenly divided into six parts. This is the simplest method to describe a fraction.
The entire is the pie, and the separate slices are the pieces that make up the whole. Our denominator is six because we have equal-sized pieces to one whole.
We have one-sixth (1/6) of the pie if we eat one piece. The comparison of two slices is two-sixths (2/6), etc.
This is a rather straightforward concept in and of itself. There are, nevertheless, various sorts of fractions and methods for solving each kind of fractional equation.
Some Key Facts About Fractions
It is really crucial to master the fundamentals before learning how to operate with fractions. Let’s start with the three main kinds of fractions:
Definitions and Examples of Fractions
Proper fraction: Generally speaking, a proper fraction is one in which the denominator is more than the numerator in value. Proper fractions include 1/2, 10/15, and 85/100, to name a few. A valid fraction’s total value, in any case, is always less than one.
Improper fraction: The value of the denominator in an improper fraction is less than the value of the numerator. Improper fractions include 6/3, 25/18, and 50/20, to name a few. An incorrect fraction’s total value, in any instance, is always more than one.
Mixed fractions: These fractions are typically written as a whole number followed by a fractional number, for instance, 223, 645, or 2558. Mixed numbers are another name for mixed fractions.
Key Terms About Fraction
Now that we have just learned about the various forms of fractions, let’s look at several additional crucial phrases and terms about fractions:
Equivalent fractions: These are basically a type of fractions that have the same value but seem to be distinct. 2/3, for instance, is just the same as 4/6.
Simplified fractions: These are generally a type of fractions that have been lowered to their simplest form. In other words, a lower fraction’s lower counterpart. 2/3 is a simplified form of 4/6 in the instance above.
Reciprocals – When the denominator is placed above the numerator, the fraction is overturned. The reciprocal of 2/3, for instance, is 3/2. When multiplying and dividing fractions, reciprocals are employed (5 1/5 is just the same as 5 x 5 or 5 x 5/1).
To improve your understanding of fractions, it’s important to familiarize yourself with key terms like numerator, denominator, equivalent fractions, and improper fractions. You can test your knowledge by checking out the calculators section on Hood MWR, which includes a handy fraction calculator tool to help you with all your calculations.
10 Simplest Ways to Calculate Fractions
Below are some easy ways you can use to calculate fractions. They are really simple and anyone can apply. Otherwise, you can use an online fraction calculator for more convenience.
How to Make an Improper Fraction from a Mixed Fraction
A mixed fraction is basically made up of a whole number and a fractional number, as previously stated. The mixed fraction of seven and four-fifths expressed numerically as 745 will be used in this instance.
When requested to make an improper fraction from a mixed fraction, they should use the following formula:
- Firstly, multiply the full amount by the fractional part of the denominator.
- Then, add the resulting number to the numerator of the fraction.
Put the final value above the old denominator as your new numerator. You now have your improper fraction.
Example:
Using the mixed fraction of 7 ⅘ as a starting point:
The fractional denominator is multiplied by the whole number: 35 = 7 x 5
To the fractional numerator, simply add the result: 39 = 35 + 4
Overlap it on top of the initial denominator: 39/5
As a result, the right response is 7 ⅘ = 39/5.
Converting Fractions to Decimals
A decimal is simply another way of describing a fraction, as both are used to recognize values less than one.
An easy division is often used to convert a fraction to a decimal: simply divide the numerator by the denominator.
Instance:
Let’s take the fraction 4/10 as an example. To have the decimal number, simply divide the numerator by the denominator:
4 ÷ 10 = 0.4
Think of the line dividing the numerator and the denominator as a division mark to understand how to convert fractions to decimals.
Converting Fractions to Percentages
In order to convert a fraction to a percentage, you can use the three simple methods as below. I will go over all of them using the same 6/20 fraction.
Method 1: To convert a percentage, divide the numerator by the denominator. After that, simply multiply the result by 100:
6 x 20 = 0.3
0.3 x 100 = 30%
Method 2: Divide the denominator by the numerator after multiplying the numerator by 100:
6 x 100 = 600
600 ÷ 20 = 30%
Method 3: Simply divide the numerator by the denominator. After that, in your final answer, just move the decimal point two places to the right:
6 ÷ 20 = 0.3
The conversion of 30% is obtained by moving the decimal point.
Please don’t forget to include the percent symbol in your final answer when converting a fraction to a percentage.
How to Multiply Fractions
When the denominators are the same, the method of adding fractions is simple.
Take 1/5 + 3/5 as a starting point. Because the denominators are equal in this situation, just add the numerators of both fractions, using the lower number of 5:
1 + 3 = 4
As a result, 1/5 + 3/5 = 4/5.
When adding fractions with non-tallying lower numbers, you must first identify the lowest popular denominator. This is the smallest number that can be divided evenly by both denominators.
Instance: 2/3 + 1/4
The lowest number that could be divided by both 4 and 3 is 12. This is the numerator of your common denominator.
Now, you must discover analogous fractions using the number 12 as the bottom number.
To convert 4 to 12, simply multiply it by 3, hence the numerator must likewise be multiplied by 3 to maintain the fraction equal:
4 x 3 equals 12 and 1 x 3 equals 3.
As a result, your corresponding fraction to 1/4 is 3/12.
Apply the same procedure to the second fraction:
3 x 4 equals 12 and 2 x 4 equals 8.
8/12 is your comparable fraction to 2/3.
Just now, add the numerators and divide by 12 to get the final answer:
3 + 8 equals 11
As a result, 8/12 + 3/12= 11/12.
11/12 is the right answer to the equation 2/3 + 1/4
How to Subtract Fractions
When the denominators are all the same, subtracting fractions is as simple as adding them. It is as simple as subtracting the second numerator from the first one while maintaining the bottom figure.
Consider the equation 4/9 – 3/9. Simply subtract 3 from 4 because you have a common denominator:
1 = 4 – 3
As a result, 4/9 – 3/9 = 1/9.
Let’s now take a look at how to subtract fractions with different denominators with the example down below.
Instance:
Consider the formula 6/5 – 2/3.
To begin, determine the lowest common denominator, which in this case is 15.
Let’s now find the equivalent fractions:
6/5 turns into 18/15. (multiply both sides by 3)
2/3 turns into 10/15. (multiply both sides by 5)
Now you may subtract the numerators:
18 – 10 – 8
As a result, 18/15 – 10/15 = 6/15.
So, 6/15 is the final answer to the equation 6/5 – 2/5.
How to Divide Fractions
In order to divide one fraction by the other, simply change the denominator and numerator of the dividing fraction to a reciprocal.
Instance:
Let’s take 1/5 ÷ 1/2 as an example. So, the latter fraction as a reciprocal in this case is 2/1
Now multiply your initial fraction by the reciprocal of your reciprocal:
1/5 x 2/1
Then, multiply both the numerators and the denominators to achieve this:
1 x 2 = 2 (numerators)
5 x 1 = 5 (denominators)
As a result, 1/5 x 2/1 = 2/5
2/5 is the final answer to the equation 1/5 ÷ 1/2
If you need help with converting units of measurement, try using the Cups and mL Converter. This calculator can quickly convert between cups and milliliters, helping you to improve your baking and cooking game.
How to Multiply Fractions
The procedure for calculating fractions as multiplications of each other is straightforward:
Firstly, multiply the numbers in your numerators.
Then, multiply the numerators by the denominators.
Overwrite your new denominator with your new numerator.
Instance:
Using 1/3 x 18 as an instance equation:
1 x 1 = 1 (numerators)
3 x 8 = 24 (denominators)
So, 1/24 is the final answer to 1/3 x 1/8.
How to Simplify a Fraction
A fraction is simplified when it is reduced to its simplest form. To put it another way, the goal is to find the smallest comparable fraction feasible.
Firstly, you need to find the most common factor. This is always the highest whole number with a divisible numerator and denominator.
To do so, just write down all of the elements for both parts of your fraction, as illustrated in the instance down below using the fraction 32/48:
The factors of 32 include: 1, 2, 4, 8, 16, and 32
The factors of 48 include: 1, 2, 3, 4, 8, 12, 16, 24, 48
So, here’s the most common factor: 16
To determine your simplified fraction, simply divide both the numerator and denominator by this figure:
Numerators: 2 = 32 ÷ 16
Denominators: 3 = 48 ÷ 16
As a result, the reduced version of 32/48 is 2/3.
Note: Always simplify your final answer to the simplest form available when solving any fractional problem.
If you want to simplify a fraction, you can use an online percentage calculator to find the equivalent percentage of the fraction. This can help you easily compare and simplify fractions with different denominators.
How to Calculate Quantity Fractions
Simply divide the supplied amount by the denominator of the fraction. After that, multiply this number by the numerator when provided a value and request to calculate a fractional component.
Instance:
You have 55 candies and wish to give 2/3 of them to your friend to take home. How much candy would he eat?
Simply divide the supplied amount by the denominator of the fraction: 55 ÷ 5 = 11
Then multiply the numerator by this figure: 2 x 11 = 22
As a result, the proper response is: 22 candies
How to Calculate Comparable Fractions
If you want to know if two fractions are comparable, divide or multiply both components of one fraction by the very same whole number.
If both of your responses are whole numbers, the fraction maintains its value and is comparable.
Instance:
To figure out if 4/5 is comparable to 12/15 or not, simply divide both 15 and 12 by a whole number.
15 ÷ 2 = 7/5
12 ÷ 2 = 6
Because you don’t have a whole number as a final answer, go to the next main number:
15 ÷ 3 = 5
12 ÷ 3 = 4
So, this demonstrates that the fractions 4/5 and 12/15 are comparable.
Besides, you can easily multiply both halves of the smaller fraction to get the answer:
5 x 3 = 15
4 x 3 = 12
To put it another way, if one fraction is a simplified form of another, they are comparable.
Frequently Asked Questions
Now, I will give answers to several commonly asked questions about fraction calculating as a final part before concluding this article.
What is the most straightforward way of calculating fractions?
Multiply every part of a fraction by the other fraction’s denominator to discover a common denominator. To obtain a common denominator for 1/5 + 2/3, for instance, multiply the 1 and 5 by 3 and the 2 and 3 by 5. As a result, you will get 3/15 + 10/15 as a result. The fractions could then be calculated.
What is the best way to divide fractions?
In order to divide fractions, just multiply the first fraction by the second fraction’s reciprocal. The reciprocal result is calculated by inverting the numerator and denominator of the fraction.
What is the best way to convert decimals to fractions?
In order to convert a finite decimal number (also known as a point number), for instance, 1.684, into a fraction, you just need to take a few steps as follows. Firstly, remove the decimal (also known as point sign) from the relevant decimal number, which in our instance will result in 1.684 being converted to 1684. After that, write a 1 in the fraction’s denominator, followed by as many zeros as there are points after the decimal place of the relevant value in the denominator. Because 1.684 includes 3 decimal place digits following the “.” in my example, my denominator would be 1000. As a result, the fraction equivalent of 1.684 is 1684/1000.
How do you calculate a quarter of a number?
As you might know,1/4 is the fraction counterpart of one fourth. As a result, it is considered a quarter of a dollar. Fourths are computed by adding two numbers by four.
What is the relationship between the concept of time and decimals?
Converting hours and minutes to decimal numbers (and vice versa) is largely employed in industrial and real-world contexts to explain as well as record time.
How can I turn a fraction into a decimal?
There are two methods for converting a fraction to a decimal value.
A power of ten can be created by either decreasing or expanding fractions. That is, powers of ten can be calculated by dividing or multiplying the denominator and numerator by the same number.
In case the denominator of the fraction already contains a 10, 100, 1000, etc. (power of ten), one can produce a 10, 100, 1000, etc. in the denominator by simply shortening or expanding the fraction such that the literal division of the fraction’s denominator and numerator better meets the conversion.
Conclusion
Fractions are simply numerical values that allow us to divide a whole into equal parts.
They are available in mixed, improper, and proper fractions and may simply be converted to percentages and decimal points.
The strategies for solving fractional equations vary according to the context, and each must always be carefully practiced, ensuring that you thoroughly comprehend the subject and demonstrate your reasoning as you go.
Even though the fundamental rules may appear intimidating at first, learning them will help you grasp how to calculate fractions effortlessly.
