Knowing how to compute a percentage of a number is essential in a variety of situations. For instance, you might have to know how to compute a percentage in order to make a student loan payment or figure a deposit on a house.
In business, percentage computations are crucial and are utilized in a variety of professional environments, such as when figuring taxes or employee bonuses. We will look at some major parts of this article, including what a percentage is, how to work out different elements of a percentage, and the various kinds of percentages.
Percentage Calculators
Just like it’s important to know how much gold you’ve got, if you’re trying to work out percentages, it can be a lot easier if you use a calculator. You can find percentage calculators on many websites but this one is quick and simple.
If you are looking to calculate your daily calorie intake, the calorie calculator on Hood MWR can help. This tool allows you to calculate how many calories you need to consume daily based on your age, gender, height, weight, and activity level. It also provides a breakdown of macronutrients and a visual representation of the calorie distribution.
What is 25% of 200?
25% of 200 is 50
Use the following percentage caculator below:
What is the percentage of a number?
Usage: Just fill up the number and percentage, and enter for the result will show off immediately.
What Percent of 200 is 50?
What is the percent of a number is another number?
If you’re curious about how many miles you’re walking or running each day, this steps to miles calculator is a helpful tool. It allows you to input your total steps for the day and then calculates the distance you’ve covered in miles. This is particularly useful for individuals who are trying to hit a specific mileage goal or overall fitness level.
50 is 25% of How Much?
What number is a certain percentage?
More Complex Percentage Calculation
So, What is the Percentage?
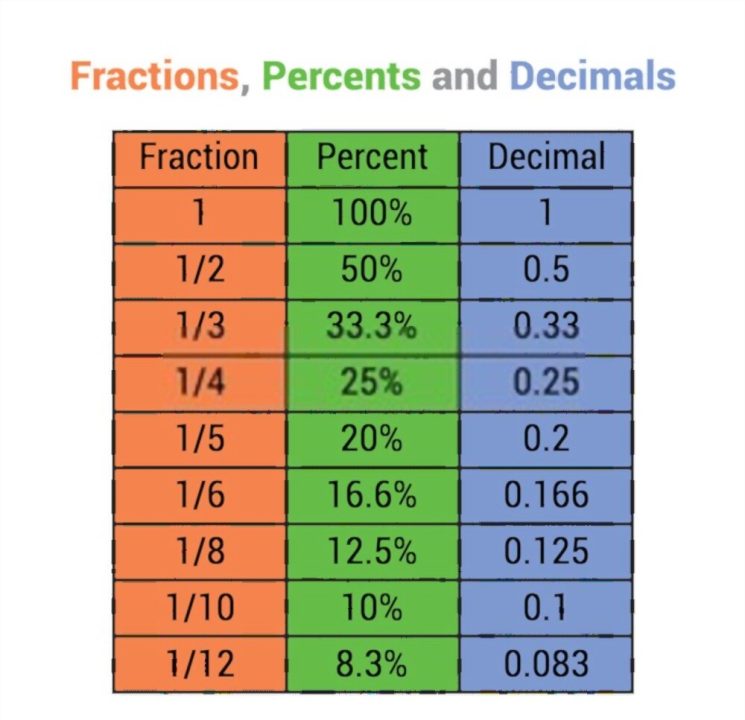
A percentage, often known as a percent, is basically a fraction of a number that is less than 100 percent. The percentage indicates a portion of an entire value and implies “per one hundred.”
Sixty-four percent, for instance, equals 64 out of 100, or 64 percent of the entire amount.
“Out of 100” or “per each 100” are other terms for percentage.
You may say “it rained 25 days out of every 100 days” or “it rained 25% of the time,” for instance.
A percentage can be expressed in a variety of ways. A decimal representation of a percentage is one way to write or represent it.
Forty-six percent, for instance, could be expressed as .46. Then divide the percentage by 100 in order to get the decimal form of the percentage. The percent symbol or ” percent ” could also be used to represent a percentage.
If you’re struggling to calculate percentages, use the Easy Fraction Calculator to make it a simple and stress-free process. Whether you need to calculate simple or complicated fractions, this tool can help.
Percentage Calculation
Working out a percentage is the process of determining the proportion of the whole in terms of 100. There are basically two methods for calculating a percentage:
- The unitary technique is used.
- By adjusting the fraction’s denominator to 100.
It should also be highlighted that in circumstances where the denominator is not a factor of 100, while the second technique of calculating the percentage is not actually applied. So, we apply the unitary technique in such conditions.
How do I calculate a percentage?
In general, the term “percent” is just another term for “hundredths.” As a consequence, 1 percent equals one-hundredth of a percent, which is 1 percent =1/100=0.01.
Let’s use the two basic methods listed above to compute the percentage.
As only two or more numbers sum up to 100, the percentage of those particular values to the whole value equals that number. Sarah, for instance, bought tiles in three distinct tones for her home. The following table lists the specifics of the buying.
| Color | The number of tiles | Rate per hundred | Fraction | Written as | Read as |
| Green | 26 | 26 | 26/100 | 26% | 26 percent |
| Yellow | 39 | 39 | 39/100 | 39% | 39 percent |
| Red | 35 | 35 | 35/100 | 35% | 35 percent |
Because the total number of items equals 100, the percentages are simple to calculate.
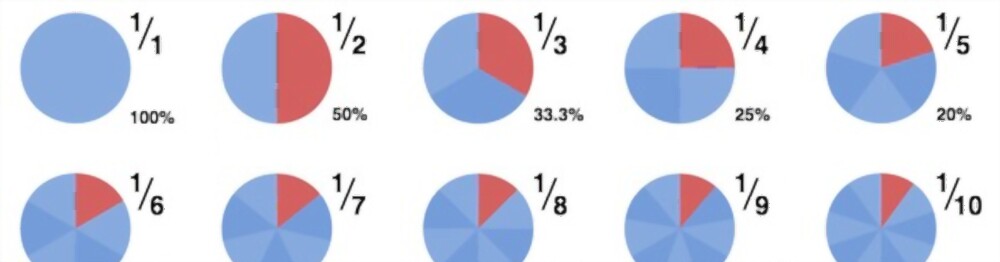
What happens if the total number of things doesn’t equal 100? We transform the fractions to corresponding fractions with a denominator of 100 in such circumstances.
Jane, for instance, wears a wristband with 20 beads in two different colors: blue and orange. Take a look at the table below, which displays the percentage of blue and orange beads out of a total of 20 beads.
Nancy and Jennifer, Jane’s sisters, also calculated the percentages but in various methods.
Nancy employed the unitary method to solve her problem. Using the unitary method of percentage calculation, we may state that there are eight red beads out of a total of 20. As a result, the number of blue beads will be 8/20 x 100= 40% of the total.
Jennifer multiplied the numerator and denominator of the fraction 8/20 by 5/5 to get the corresponding fraction 40/100.
As a result, 8/20=(85)/(205) = 40/100 = 40%
In a nutshell, there are three fundamental methods for calculating percentages:
A percentage could also be calculated in several various ways. A popular technique for calculating the percentage of anything is to use the formula below:
1. Calculate the entire or total amount of what you are looking for a percentage for
If you wish to compute the percentage of how many days it snowed in a month, for instance, the total amount will be the number of days in that month. Now, let’s say we are assessing the amount of snow that fell in December, a month with 30 days.
2. Take the number you want to calculate the percentage for and divide it by two
Let’s imagine it snowed 15 out of the 30 days in December, like in the instance above. You would take 15 and divide it by 30 to get 0.5.
3. Take the value from step two and multiply it by 100
Using the same instance as before, you will multiply 0.5 by 100. This is equivalent to 50, giving you a 50 percent answer. As a result, it snowed 50% of the time in December.
Percentage Calculation Formula
To work out the percentage of a whole in terms of 100, simply use the percentage formula. You could relate to a number as a fraction of 100 using this simple formula. If you look closely, you will notice that all three methods for calculating percentages indicated above can be readily calculated using the formula as below:
(Value/Total Value)/100 = Percentage
Calculating percentages can be tricky, but our online percentage calculator makes it easy for you to find any percentage of a given number. Whether you’re trying to figure out a sale price or a tip, this tool is a great resource to have on hand. With just a few clicks, you can calculate any percentage you need and get accurate results in seconds.
The Difference in Percentage Between Two Numbers
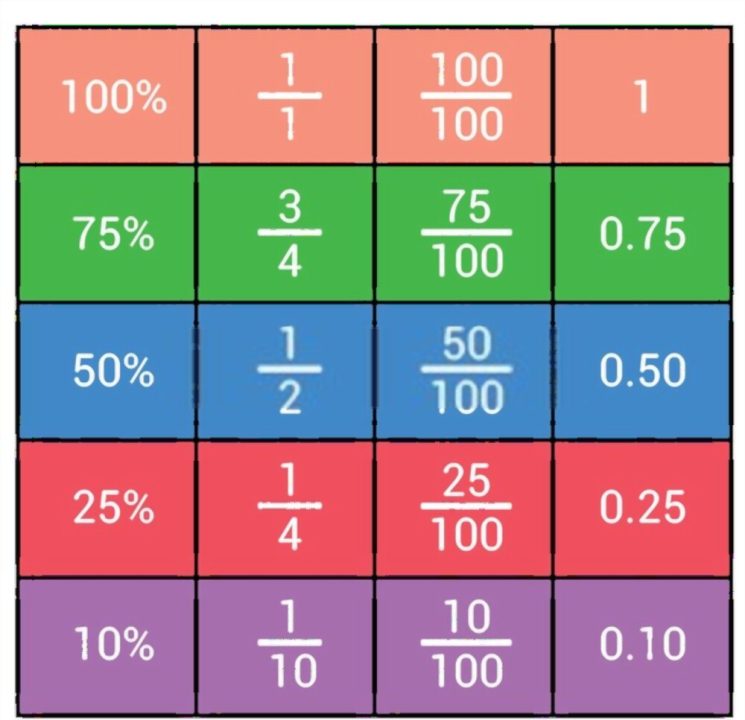
The percentage difference is generally the variation of a quantity over time expressed as a percent change. Sometimes we might need to know how much something has increased or decreased in percentages, which is considered to be a Percentage Change. For instance, a rise in population, and alleviation of poverty, etc.
We have a basic formula to indicate the % change in quantity. When computing percentage differences, there are three scenarios that may occur:
- Find the increase in the percentage
- Find the reduction in the percentage
- Find the percentage difference
What is the formula for calculating a percentage increase?
When a quantity is increased over the years, the percentage rise relates to the purchase fluctuations in the value. For instance, a growth in population, an increase in the number of microbes on a surface, and so on. The formula down below might be used to compute the percentage increase:
(Increased Value-Initial Value)/Initial Value 100 = Percentage Increase
What is the formula for calculating a percentage decrease?
When a value is decreased after a while, the percentage decline relates to the perchance fluctuations in the value. For instance, a drop in snowfall, a drop in the number of Covid sufferers, and so on. The formula down below might be used to compute the percentage decrease:
(Initial Value-Decreased Value)/Initial Value x 100 = Percentage Decrease
Key Things to keep in mind: To work out the percentage of the whole, simply multiply the value of one percent by the percent we are looking for.
- A percentage could also be used to describe a decrease or increase in any quantity.
- Converting percentages to fractions and vice versa is possible.
- Percentages can be changed back and forth. For instance, 25 percent of 40 equals 40 percent of 25.
To calculate a percentage decrease, use the formula: ((Original Value – New Value) / Original Value) x 100. This can be useful in tracking changes in measurements over time or to compare pricing for budgeting. Check out the Easy Fraction Calculator for help with converting fractions to percentages.
What is the formula for calculating the percentage difference?
Percentages can be used to compare two things that are connected to one another. For instance, you could wish to compare the price of a product last year to the price of a similar item this year. The % difference between the two item prices can be calculated using this formula.
The formula for calculating a percentage difference is as follows: |V1 – V2|/ [(V1 + V2)/2] x 100
V1 equals the cost of one item, and V2 equals the cost of the second item in this calculation.
The following is an instance of how to use this formula to find out the difference in unit cost: Last year, an item cost $20, and this year, a similar item cost $30. To get the percentage difference, simply subtract the costs from each other as follows: 30 minus 20 equals 10. So, the average of these two expenses will then be calculated (20 + 30 / 2 = 25). After that, divide five by 25 to get 0.33. Then multiply 0.33 by 100 to get 33. This signifies that the price of the item this year is 33% higher than the price of the item last year.
Different Types of Percentage Issues
In both individual and professional situations, there are three basic sorts of percentage concerns to be aware of. These are some of them:
- Figuring out the first number
- Figuring out the final number
- Figuring out the percentage
Whether you are dealing with percentages related to body weight, basal metabolic rate, or military service, knowing how to calculate percentages is crucial. Use our percentage calculator to effortlessly calculate percentages needed for weight loss, weight gain, or other fitness related issues.
Working out the starting number
“45 percent of what is 2?” is an example of a percentage issue that asks you to discover the initial number. This is a more complex calculation to solve, although it is simple to do so using the formula already given. You should divide the whole by the percentage given in this sort of percentage issue. If the question is “What is 45 percent of 2?” you will divide two by 45 percent, or .45. This gives you 4.4, indicating that 2 is 45 percent of 4.4.
Working out the ending number
An instance of a question that might require you to perform a percentage calculation to get the ending number in an issue is the following: “How much is 50% of 25?” You already have the % and the total amount that you wish to figure out a percentage of for this challenge.
As a result, you would go to the second stage, which is detailed in the preceding section. Nevertheless, because you already have the percentage, you should multiply it by the total number rather than divide it. You will multiply 50 percent, or 0.5, by 25 in this calculation. This will then give you a 12.5% answer. As a result, the answer to this percentage question is “50% of 25 is 12.5.”
Working out the percentage
A question like “What the percentage of 5 is 2” can be used to solve a percentage issue where you’d have to calculate the percentage. In this case, you will have to calculate in percentages how much of 2 is in the total of 5. You can simply solve this problem just by dividing the number you want to convert into a percentage by the whole. As an instance, divide two by 5 in this case. 0.4 is the result of this equation. The result of multiplying 0.4 by 100 is 40, or 40 percent. As a result, two is equivalent to 40% of 5.
FAQs
How do you calculate ratios from percentages?
To calculate a ratio from a percentage, you need to convert the percentage to a decimal and then simplify the ratio. For example, if you have a percentage of 50%, you would convert it to 0.5 and then simplify the ratio.
What is the formula for percentage calculation?
The formula for percentage calculation is: (part/whole) x 100%. This formula can be used to find the percentage of a number or to find the part of a number that represents a certain percentage.
How is the ratio calculated in a calculator?
To calculate a ratio in a calculator, you would divide one number by another number and then simplify the ratio. For example, if you have a ratio of 2:3, you would divide 2 by 3 and then simplify the ratio to 2/3.
What is a 2 to 3 ratio percentage?
A 2 to 3 ratio percentage would be 40%. This is because you would divide 2 by the total of 2+3, which is 5, and then multiply by 100%.
What is 25% as a ratio?
25% as a ratio is 1:4. This is because you would divide 25 by 100 to get 0.25, and then simplify the ratio by dividing both sides by 0.25.
What is 75% as a ratio?
75% as a ratio is 3:4. This is because you would divide 75 by 100 to get 0.75, and then simplify the ratio by dividing both sides by 0.75.
How do you find 30% of 90?
To find 30% of 90, you would multiply 90 by 0.3, which is the decimal equivalent of 30%. This would give you an answer of 27.
How do you work out 40% of 80?
To work out 40% of 80, you would multiply 80 by 0.4, which is the decimal equivalent of 40%. This would give you an answer of 32.
What is the percentage analysis method?
The percentage analysis method is a technique used to analyze financial statements by calculating the percentage of each item in relation to a base item. This method is used to compare financial statements over time or between companies.
How do you find 30% of 120?
To find 30% of 120, you would multiply 120 by 0.3, which is the decimal equivalent of 30%. This would give you an answer of 36.
What is 25% out of 100?
25% out of 100 is 0.25. This is because you would divide 25 by 100 to get the decimal equivalent of 0.25. (source: Math is Fun)
Is it possible for 20% of 45 to be 9?
Yes, it is possible for 20% of 45 to be 9. To check, you would multiply 45 by 0.2, which is the decimal equivalent of 20%. This would give you an answer of 9.
How do you find 15% of $60?
To find 15% of $60, you would multiply 60 by 0.15, which is the decimal equivalent of 15%. This would give you an answer of $9.
What is 20% of 90 out of 100?
20% of 90 out of 100 is 18. This is because you would multiply 90 by 0.2, which is the decimal equivalent of 20%.
How do you work out 15% of 120?
To work out 15% of 120, you would multiply 120 by 0.15, which is the decimal equivalent of 15%. This would give you an answer of 18.
